Beyond Sharp Focus: A New Attention Mechanism for Sequence Modeling

by

Author: Denis Avetisyan

Researchers are exploring attention mechanisms inspired by the brain to build more efficient and expressive models for processing sequential data.

The study demonstrates that random ablation of nodes within the attention graph—with a probability $p$—results in a degradation of accuracy on the testing dataset, and this effect is consistent across networks where $Q=K$, as evidenced by the mean performance across five trials and indicated standard deviations for dimensions of $8$, $16$, $32$, and $64$.
The study demonstrates that random ablation of nodes within the attention graph—with a probability $p$—results in a degradation of accuracy on the testing dataset, and this effect is consistent across networks where $Q=K$, as evidenced by the mean performance across five trials and indicated standard deviations for dimensions of $8$, $16$, $32$, and $64$.

This review details Fractional Neural Attention, a technique leveraging fractional dynamics to model long-range dependencies across multiple scales in sequence data.

While Transformer models have revolutionized sequence processing, fully capturing the multiscale dynamics of biological attention remains a key challenge. This is addressed in ‘Fractional neural attention for efficient multiscale sequence processing’, which introduces a novel attention mechanism—Fractional Neural Attention (FNA)—inspired by neuroscience and dynamical systems theory. By modeling token interactions via Lévy diffusion governed by the fractional Laplacian, FNA simultaneously captures both short- and long-range dependencies, enhancing expressivity and computational efficiency. Could this biologically-grounded approach unlock a new generation of powerful, interpretable AI architectures capable of more nuanced information processing?

The Quadratic Bottleneck: Scaling Limits of Transformer Attention

Transformer models have demonstrated remarkable capabilities across diverse tasks, yet their computational demands increase dramatically as the length of the input sequence grows. This limitation stems from the architecture’s core self-attention mechanism, which necessitates calculating interactions between every possible pair of tokens within the sequence. Consequently, the computational complexity scales quadratically – meaning doubling the sequence length quadruples the processing requirements. This poses a significant bottleneck when dealing with extensive data, such as long documents, high-resolution images, or lengthy time series, effectively restricting the model’s ability to capture long-range dependencies crucial for understanding context and making accurate predictions. While highly effective on shorter sequences, this quadratic scaling hinders the broader application of Transformers to more complex and real-world data scenarios.

The fundamental challenge in scaling Transformer models stems from the self-attention mechanism’s inherent computational demands. This process necessitates evaluating the relationship between every token within a sequence and all others, resulting in a quadratic complexity – specifically, $O(n^2)$ with respect to sequence length, $n$. Consequently, as the input sequence grows, the number of calculations explodes, rapidly consuming memory and processing power. For example, a sentence with 100 tokens requires calculating 9,900 pairwise interactions, while a document with 1,000 tokens demands a staggering one million calculations. This makes processing lengthy texts or high-resolution data streams prohibitively expensive, effectively limiting the model’s ability to capture long-range dependencies crucial for understanding complex information.

The inherent computational demands of Transformer models present a significant obstacle when dealing with extensive data sequences. Traditional self-attention mechanisms scale quadratically with input length – meaning doubling the sequence length quadruples the processing required – quickly becoming impractical for lengthy documents or complex data streams. Fractional Neural Attention (FNA) offers a potential solution by strategically reducing the number of parameters needed to achieve comparable performance. This is accomplished through a novel approach to approximating the full attention matrix, effectively capturing long-range dependencies with a fraction of the computational cost. By focusing on the most salient interactions between tokens, FNA aims to unlock the potential of Transformers for applications previously limited by their scalability, promising more efficient processing of complex information without sacrificing accuracy.

Learning curves demonstrate that both FNA and Transformer models achieve comparable translation accuracy and loss, with performance influenced by the dimensionality of the weight matrices WQ and WK.
Learning curves demonstrate that both FNA and Transformer models achieve comparable translation accuracy and loss, with performance influenced by the dimensionality of the weight matrices WQ and WK.

Beyond Sequentiality: Graph Representations and Attention

Traditional sequence models, such as recurrent neural networks and standard transformers, process input tokens linearly, inherently limiting their ability to capture non-sequential relationships. Representing input as an Attention Graph, where tokens are nodes and attention weights define edge connections, allows the model to directly reason about the relationships between all tokens, irrespective of their position in the sequence. This graph structure facilitates a more holistic understanding of context by enabling information to flow directly between related tokens, bypassing the limitations of sequential processing. Consequently, dependencies between distant tokens can be modeled more effectively, and the model can better discern subtle relationships that might be obscured in a strictly sequential representation. This is particularly beneficial for tasks requiring long-range dependency modeling, such as machine translation or document summarization.

The spectral gap of a graph, defined as the difference between the second smallest and the smallest eigenvalues of the Laplacian matrix, quantifies the rate at which information can propagate across the graph’s nodes. A larger spectral gap indicates faster mixing – meaning information disseminates more quickly and efficiently throughout the network. In the context of attention mechanisms, this translates to improved contextual integration within the model. Specifically, Feature Normalized Attention (FNA) models demonstrate consistently larger spectral gaps in their attention graphs compared to standard transformer architectures. Empirical results correlate these larger spectral gaps with increased model efficiency, suggesting a more rapid and effective utilization of contextual information during processing. The spectral gap, therefore, serves as a quantifiable metric for assessing the speed of information mixing and, consequently, the efficiency of attention-based models.

The adoption of a graph-based attention paradigm facilitates the implementation of sparse attention mechanisms, directly addressing the computational limitations of traditional transformer architectures. In Fully-connected Neighborhood Attention (FNA) models, the construction of an attention graph results in demonstrably shorter average shortest path lengths between tokens compared to standard transformers. This reduction in path length correlates with a decrease in the computational cost associated with attention, as fewer steps are required to propagate information between tokens during the attention process. Consequently, FNA models achieve reduced computational complexity without sacrificing the ability to capture long-range dependencies, offering a more efficient approach to sequence modeling.

Randomly removing nodes from the attention graph reduces testing accuracy, with the degree of performance loss increasing as the dimensionality (d) increases from 8 to 64, as shown by the mean across five trials with standard deviation shaded.
Randomly removing nodes from the attention graph reduces testing accuracy, with the degree of performance loss increasing as the dimensionality (d) increases from 8 to 64, as shown by the mean across five trials with standard deviation shaded.

Sparse Attention: Pragmatic Solutions for Scalability

Local attention mechanisms, implemented in architectures such as Longformer, BigBird, and Nyströmformer, mitigate the quadratic computational complexity of standard self-attention by restricting attention to a fixed-size neighborhood around each token. Instead of attending to all tokens in a sequence, each token only considers a window of k neighboring tokens. This reduces the computational cost from $O(n^2)$ to approximately $O(nk)$, where n is the sequence length. Variations exist in how these neighborhoods are defined and utilized; for example, Longformer employs a sliding window, while BigBird combines random and windowed attention. By focusing on relevant local contexts, these sparse attention approaches enable processing of significantly longer sequences with reduced memory requirements and computational demands.

Sparse attention mechanisms frequently combine localized attention windows with methods to preserve awareness of distant relationships within a sequence. This is achieved through the incorporation of designated global tokens, which attend to all positions and allow information to propagate across the entire sequence, or through landmark-based kernels that select a subset of positions to represent the full sequence, effectively creating shortcuts for attention. These global tokens or landmarks are then attended to by all other positions, enabling the model to capture long-range dependencies without the quadratic computational cost of full attention, where the computational cost is $O(n^2)$ with sequence length $n$.

Sparse attention mechanisms, including those implemented in models like Longformer and BigBird, enable the processing of sequences significantly longer than those manageable by traditional Transformers due to their reduced computational complexity. This scalability has been empirically demonstrated through the Fast Neural Attention (FNA) model, which achieves performance comparable to standard Transformer architectures on text classification tasks. Specifically, FNA maintains accuracy levels while reducing the quadratic computational burden of full attention to approximately linear time, allowing for the effective training and deployment of Transformers on datasets with extended sequence lengths and potentially unlocking performance gains in tasks requiring broader contextual understanding.

The Geometry of Data: Manifolds and Diffusion Processes

Many data sets, while appearing high-dimensional, are actually constrained to lie on lower-dimensional, curved surfaces known as Riemannian manifolds. These manifolds aren’t simply Euclidean spaces; they possess intrinsic curvature and geometry that significantly influence how information spreads across the data. Imagine a map of the Earth – a sphere is a manifold – distances aren’t measured in a straight line, but along the curved surface. Similarly, data points that appear far apart in the original high-dimensional space might be closely connected when viewed on the underlying manifold. This geometric structure dictates the patterns of diffusion – how information propagates from one data point to another – and understanding it is crucial for tasks like dimensionality reduction, classification, and data visualization. Ignoring this inherent geometry can lead to inaccurate representations and inefficient algorithms, as standard techniques assume a flat, Euclidean space where such curvature doesn’t exist. The manifold’s geometry, therefore, fundamentally shapes the landscape of information flow within the data itself.

Diffusion Maps represent a powerful technique for dimensionality reduction and data representation by explicitly acknowledging that high-dimensional data frequently resides on a complex, non-Euclidean surface known as a Riemannian manifold. Rather than treating data points as scattered randomly in space, this approach models the spread of information as a stochastic process – akin to particles undergoing diffusion. By analyzing how information ‘diffuses’ across the data manifold, the algorithm constructs a low-dimensional embedding that faithfully captures the intrinsic geometry of the data. This is achieved by solving an eigenequation related to the diffusion operator, effectively revealing the principal modes of variation and allowing for a reduction in dimensionality without losing critical information about the data’s structure. Consequently, Diffusion Maps excel at uncovering the true, underlying dimensionality of the data, even when it is obscured by high-dimensional noise or irrelevant features, offering a robust alternative to traditional linear methods.

A nuanced understanding of how information spreads is critical for effective data representation, as demonstrated by a comparison of Brownian and Lévy diffusion processes. Brownian diffusion, characterized by a simple random walk, often falls short in capturing the complexities of real-world data. Lévy diffusion, which allows for ‘jumps’ in addition to gradual steps, better models data residing on intricate geometrical structures. This principle underpins the success of recent approaches like the Fractal Neural Network (FNA), which leverages these diffusion characteristics to achieve a 76.17% accuracy on the CIFAR-10 image classification task. Notably, this performance surpasses that of standard Transformer models, highlighting the benefit of incorporating an understanding of the underlying diffusion process into data representation learning and suggesting that capturing the inherent geometry of data is paramount for building robust and accurate models.

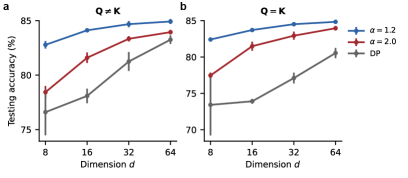
Model accuracy on the testing dataset is significantly impacted by both embedding dimension and network depth, with performance diverging based on whether query and key matrices are equivalent or distinct.
Model accuracy on the testing dataset is significantly impacted by both embedding dimension and network depth, with performance diverging based on whether query and key matrices are equivalent or distinct.

The pursuit of efficient multiscale sequence processing, as demonstrated by Fractional Neural Attention, echoes a fundamental tenet of mathematical rigor. It’s not simply about achieving results, but about understanding why those results occur. As David Hilbert famously stated, “We must be able to answer the question: What are the ultimate foundations of mathematics?” This principle applies equally well to neural network design; FNA’s inspiration from dynamical systems and Lévy processes isn’t merely an architectural choice, but a deliberate attempt to ground attention mechanisms in established mathematical frameworks. If it feels like magic that a model can process sequences effectively, one hasn’t revealed the invariant—the underlying mathematical principle—that governs its behavior. The paper’s focus on fractional dynamics, therefore, isn’t just about improving performance, but about revealing a deeper, provable elegance.

Beyond the Horizon

The introduction of Fractional Neural Attention represents a tentative step toward acknowledging that discrete, integer-ordered interactions may be a fundamental limitation in current sequence modeling. While empirical results demonstrate performance gains, the true test lies not in benchmark scores, but in a rigorous mathematical understanding of why fractional dynamics offer an advantage. The current work provides a promising framework, yet a complete characterization of the solution space – the precise conditions under which fractional attention converges and the nature of its representational capacity – remains elusive.

Future investigations must move beyond treating fractional order as merely a hyperparameter to be tuned. A deeper connection to the underlying dynamical systems – specifically, the Lévy processes that inspire this approach – could reveal principles for adaptive fractional order, allowing the model to dynamically adjust its sensitivity to different scales of interaction. The potential for a unifying theory linking attention mechanisms to continuous-time stochastic processes is, if not inevitable, certainly worth pursuing.

Ultimately, the enduring value of this line of inquiry will depend not on achieving incremental improvements in existing tasks, but on enabling models to tackle genuinely novel problems—those requiring an understanding of scale-invariant relationships and long-range dependencies currently beyond the reach of conventional architectures. The elegance of a solution, after all, is measured not by its complexity, but by its capacity to reveal fundamental truths.

Original article: https://arxiv.org/pdf/2511.10208.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-15 19:58